My latest posts
- 17 Nov 2022 » (with Y. Hayut) Perfect Subtree Property for Weakly Compact Cardinals
Israel Journal of Mathematics. Appeared online.
DOI: 10.1007/s11856-022-2385-4. PDF. arXiv. Bibtex. - 16 Nov 2022 » Gdansk Logic Conference - TBA
I am invited to give an invited talk at the first Gdansk Logic Conference, University of Gdansk, Poland, May 5-7, 2023.
Title and abstract of this talk will be announced in due course.
- 16 Aug 2022 » 10th Indian Conference on Logic and its Applications (ICLA) - TBA
I am invited to give an invited talk at the 10th Indian Conference on Logic and its Applications (ICLA) in Indore, India, March 3-5, 2023.
Title and abstract of this talk will be announced in due course.
- 02 May 2022 » (with P. Schlicht, D. Schrittesser, and T. Weinert) Lebesgue's density theorem and definable selectors for ideals
Israel Journal of Mathematics. Volume 249, May 2022. Pages 501-551.
DOI: 10.1007/s11856-022-2312-8. PDF. arXiv. Bibtex. - 16 Feb 2022 » Winter Meeting of the ASL with the JMM - Universally Baire Sets, Determinacy, and Inner Models
I am invited to give an invited address at the 2023 Winter Meeting of the Association for Symbolic Logic with the JMM in Boston, USA, January 4-7, 2023.
Universally Baire Sets, Determinacy, and Inner Models
Computing the large cardinal strength of a given statement is one of the key research directions in set theory. Fruitful tools to tackle such questions are given by inner model theory. The study of inner models was initiated by Gödel’s analysis of the constructible universe $L$. Later, it was extended to canonical inner models with large cardinals, e.g., measurable cardinals, strong cardinals or Woodin cardinals, which were introduced and studied by Jensen, Mitchell, Steel, Woodin, Sargsyan, and others. We will outline the role universally Baire sets play in the study of inner models and their connections to determinacy axioms. In particular, we will discuss recent results on $\mathsf{Sealing}$, a formalization due to Woodin of the statement that the theory of the universally Baire sets cannot be changed by forcing.
- 17 Jan 2022 » Core Model Seminar - A stationary-tower-free proof of Sealing
I was invited to give a series of two talks in the Core Model Seminar, an online seminar organized by Ernest Schimmerling and Benjamin Siskind, Carnegie Mellon University.
A stationary-tower-free proof of Sealing
Sealing is a generic absoluteness principle for the theory of the universally Baire sets of reals introduced by Woodin. It is deeply connected to the Inner Model Program and plays a prominent role in recent advances in inner model theory. Woodin showed in his famous Sealing Theorem that in the presence of a proper class of Woodin cardinals Sealing holds after collapsing a supercompact cardinal. In the first talk, I will outline the importance of Sealing and discuss a new and stationary-tower-free proof of Woodin’s Sealing Theorem that is based on Sargsyan’s and Trang’s proof of Sealing from iterability. In the second talk, I will outline the proof of an extension of the Sealing Theorem that gives models in which Theta is regular. This is joint work with Grigor Sargsyan.
- 15 Jan 2022 » Baltic Set Theory Seminar - A stationary-tower-free proof of Woodin's Sealing Theorem
I am invited to give a series of talks in the Baltic Set Theory Seminar, an online seminar organized by Grigor Sargsyan. The schedule as well as the zoom link appears on the seminar webpage.
A stationary-tower-free proof of Woodin’s Sealing Theorem
I will present a proof of $\mathsf{Sealing}$ from a supercompact and a class of Woodin cardinals using genericity iterations. The proof is joint work with Sargsyan and Wcisło, and builds on the work of Sargsyan-Trang.
- 03 Jan 2022 » PhDs in Logic XIII, Turin - Highlights from infinite games, mice, and their connection
I am invited to give a talk at the PhDs in Logic XIII conference in Turin, Italy, September 5 - 7, 2022.
Highlights from infinite games, mice, and their connection
The study of inner models was initiated by Gödel’s analysis of the constructible universe. Later, the study of canonical inner models with large cardinals, e.g., measurable cardinals, strong cardinals or Woodin cardinals, was pioneered by Jensen, Mitchell, Steel, and others. Around the same time, the study of infinite two-player games was driven forward by Martin’s proof of analytic determinacy from a measurable cardinal, Borel determinacy from ZFC, and Martin and Steel’s proof of levels of projective determinacy from Woodin cardinals with a measurable cardinal on top. First Woodin and later Neeman improved the result in the projective hierarchy by showing that in fact the existence of a countable iterable model, a mouse, with Woodin cardinals and a top measure suffices to prove determinacy in the projective hierarchy. This opened up the possibility for an optimal result stating the equivalence between local determinacy hypotheses and the existence of mice in the projective hierarchy. In this talk, we will outline the main concepts and results connecting determinacy hypotheses with the existence of mice with large cardinals as well as recent progress in the area.
- 02 Jan 2022 » European Set Theory Conference, Turin - Universally Baire Sets and the Inner Model Program
I am invited to give a plenary talk at the European Set Theory Conference 2022 in Turin, Italy, August 29 - September 2, 2022.
Universally Baire Sets and the Inner Model Program
Universally Baire sets originate in work of Schilling and Vaught, and they were first systematically studied by Feng, Magidor, and Woodin. Since then they play a prominent role in many areas of set theory. We will discuss recent progress on their relationship to the Inner Model Program. First, we will outline the resolution of Sargsyan’s Conjecture on the large cardinal strength of determinacy when all sets are universally Baire. The second part of the talk will focus on sealing the theory of the universally Baire sets. Woodin showed in his famous Sealing Theorem that in the presence of a proper class of Woodin cardinals $\mathsf{Sealing}$, a generic absoluteness principle for the theory of the universally Baire sets of reals, holds after collapsing a supercompact cardinal. We will outline the importance of $\mathsf{Sealing}$ and discuss a new and stationary-tower-free proof of Woodin’s Sealing Theorem that is based on Sargsyan’s and Trang’s proof of $\mathsf{Sealing}$ from iterability. The second part is joint work with Grigor Sargsyan and Bartosz Wcisło.
- 05 Oct 2021 » (with P. Lücke) Sigma_1-definability at higher cardinals: Thin sets, almost disjoint families and long well-orders
- 23 Aug 2021 » (with P. Schlicht) Uniformization and Internal Absoluteness
Accepted for publication in the Proceedings of the AMS. PDF. arXiv. Bibtex.
- 21 Aug 2021 » Set Theory Conference in Jerusalem - Inner Models, Determinacy, and Sealing
I am invited to give a talk at the conference Advances in Set Theory that will take place at the Hebrew University of Jerusalem, July 10-14, 2022.
Inner Models, Determinacy, and Sealing
Inner model theory has been very successful in connecting determinacy axioms to the existence of inner models with large cardinals and other natural hypotheses. Recent results of Larson, Sargsyan, and Trang suggest that a Woodin limit of Woodin cardinals is a natural barrier for our current methods to prove these connections. One reason for this comes from Sealing, a generic absoluteness principle for the theory of the universally Baire sets of reals introduced by Woodin. Woodin showed in his famous Sealing Theorem that in the presence of a proper class of Woodin cardinals Sealing holds after collapsing a supercompact cardinal. I will outline the importance of Sealing and discuss a new and stationary-tower-free proof of Woodin’s Sealing Theorem that is based on Sargsyan’s and Trang’s proof of Sealing from iterability. This is joint work with Grigor Sargsyan and Bartosz Wcisło.
- 20 Aug 2021 » Set Theory Workshop at the Erwin Schrödinger Institute, Vienna - Preserving universally Baire sets and Sealing
I am invited to give a talk at a Set Theory Workshop at the Erwin Schrödinger Institute that will take place in Vienna, July 4-8, 2022.
Preserving universally Baire sets and Sealing
Universally Baire sets play a central role in many areas of set theory. In inner model theory many objects we construct are universally Baire and this is crucial as it allows us to extend them onto generic extensions. Sealing, a generic absoluteness principle for the theory of the universally Baire sets introduced by Woodin, is therefore an obstruction to construct canonical inner models. In his famous Sealing Theorem, Woodin showed that in the presence of a proper class of Woodin cardinals Sealing holds after collapsing $2^{2^\kappa}$ for a supercompact cardinal $\kappa$. We will outline a new and stationary-tower-free proof of Woodin’s Sealing Theorem that is based on Sargsyan’s and Trang’s proof of Sealing from iterability. A key new technical concept in our proof is the preservation of universally Baire sets in ultrapowers by extenders. This is joint work with Grigor Sargsyan and Bartosz Wcisło.
- 19 Aug 2021 » Logic Colloquium Reykjavik, Iceland - A stationary-tower-free proof of Sealing from a supercompact
I am invited to give a talk in the special session on set theory at the Logic Colloquium 2022 taking place in Reykjavik, Iceland, June 27 - July 1, 2022.
A stationary-tower-free proof of $\mathsf{Sealing}$ from a supercompact
$\mathsf{Sealing}$ is a generic absoluteness principle for the theory of the universally Baire sets of reals introduced by Woodin. It is deeply connected to the Inner Model Program and plays a prominent role in recent advances in inner model theory. Woodin showed in his famous Sealing Theorem that in the presence of a proper class of Woodin cardinals $\mathsf{Sealing}$ holds after collapsing a supercompact cardinal. I will outline the importance of $\mathsf{Sealing}$ and discuss a new and stationary-tower-free proof of Woodin’s Sealing Theorem that is based on Sargsyan’s and Trang’s proof of $\mathsf{Sealing}$ from iterability. This is joint work with Grigor Sargsyan and Bartosz Wcisło.
- 18 Aug 2021 » Münster conference on inner model theory - A stationary-tower-free proof of Woodin's Sealing Theorem
I am invited to give a talk at the Münster conference on inner model theory that will take place June 20 - July 1, 2022.
A stationary-tower-free proof of Woodin’s Sealing Theorem
I will present a proof of $\mathsf{Sealing}$ from a supercompact and a class of Woodin cardinals using genericity iterations. The proof is joint work with Sargsyan and Wcisło, and builds on the work of Sargsyan-Trang.
- 16 Aug 2021 » Set Theory Seminar, University of Vienna - Inner Models, Determinacy, and Sealing
I was invited to give a talk in the Set Theory Seminar of the University of Vienna on May 24, 2022.
Inner Models, Determinacy, and Sealing
Inner model theory has been very successful in connecting determinacy axioms to the existence of inner models with large cardinals and other natural hypotheses. Recent results of Larson, Sargsyan, and Trang suggest that a Woodin limit of Woodin cardinals is a natural barrier for our current methods to prove these connections. One reason for this comes from Sealing, a generic absoluteness principle for the theory of the universally Baire sets of reals introduced by Woodin. Woodin showed in his famous Sealing Theorem that in the presence of a proper class of Woodin cardinals Sealing holds after collapsing a supercompact cardinal. I will outline the importance of Sealing and discuss a new and stationary-tower-free proof of Woodin’s Sealing Theorem that is based on Sargsyan’s and Trang’s proof of Sealing from iterability. This is joint work with Grigor Sargsyan and Bartosz Wcisło.
- 15 Aug 2021 » Set Theory Seminar, University of Barcelona - Inner Models, Determinacy, and Sealing
I was invited to give a talk in the Barcelona Set Theory Seminar on May 11, 2022.
Inner Models, Determinacy, and Sealing
Inner model theory has been very successful in connecting determinacy axioms to the existence of inner models with large cardinals and other natural hypotheses. Recent results of Larson, Sargsyan, and Trang suggest that a Woodin limit of Woodin cardinals is a natural barrier for our current methods to prove these connections. One reason for this comes from Sealing, a generic absoluteness principle for the theory of the universally Baire sets of reals introduced by Woodin. Woodin showed in his famous Sealing Theorem that in the presence of a proper class of Woodin cardinals Sealing holds after collapsing a supercompact cardinal. I will outline the importance of Sealing and discuss a new and stationary-tower-free proof of Woodin’s Sealing Theorem that is based on Sargsyan’s and Trang’s proof of Sealing from iterability. This is joint work with Grigor Sargsyan and Bartosz Wcisło.
- 14 Aug 2021 » Algebra Seminar, TU Wien - A journey through the world of mice and games
I was invited to give a talk in the TU Wien FG1 Seminar, the Research Seminars of the Set Theory and the Universal Algebra groups, on April 29, 2022.
A journey through the world of mice and games
This talk will be an informal and gentle introduction to the research area called “inner model theory”. I will introduce determinacy of infinite two player games and outline classical as well as recent results connecting this notion with canonical models of set theory (called “mice”). We will discuss versions of the inner model problem and why they are central to set theory together with recent results suggesting that new methods are required for major advance on these problems.
- 13 Aug 2021 » Logic Colloquium, University of Vienna - The Interplay of Determinacy, Large Cardinals, and Inner Models
I was invited to give a talk in the Logic Colloquium of the University of Vienna on March 10, 2022.
The Interplay of Determinacy, Large Cardinals, and Inner Models
The standard axioms of set theory, Zermelo-Fraenkel set theory with Choice (ZFC), do not suffice to answer all questions in mathematics. While this follows abstractly from Kurt Gödel’s famous incompleteness theorems, we nowadays know numerous concrete examples for such questions. In addition to a large number of problems in set theory, even many problems outside of set theory have been showed to be unsolvable, meaning neither their truth nor their failure can be proven from ZFC. A major part of set theory is devoted to attacking this problem by studying various extensions of ZFC and their properties with the overall goal to identify the “right” axioms for mathematics that settle these problems.
Determinacy assumptions are canonical extensions of ZFC that postulate the existence of winning strategies in natural infinite two-player games. Such assumptions are known to enhance sets of real numbers with a great deal of canonical structure. Other natural and well-studied extensions of ZFC are given by the hierarchy of large cardinal axioms. Inner model theory provides canonical models for many large cardinal axioms. Determinacy assumptions, large cardinal axioms, and their consequences are widely used and have many fruitful implications in set theory and even in other areas of mathematics. Many applications, in particular, proofs of consistency strength lower bounds, exploit the interplay of determinacy axioms, large cardinals, and inner models. In this talk I will survey recent developments as well as my contribution to this flourishing area.
- 13 Aug 2021 » (with G. Sargsyan) HOD in inner models with Woodin cardinals
The Journal of Symbolic Logic. Volume 86, Issue 3, September 2021. Pages 871-896.
DOI: 10.1017/jsl.2021.61. PDF. arXiv. Bibtex. - 12 Aug 2021 » Leeds University Models and Sets seminar - The Interplay of Determinacy, Large Cardinals, and Inner Models
I was invited to give a virtual talk in the Leeds University Models and Sets seminar on March 8, 2022. The talk will be at 13:45 local time, i.e., 14:45 Vienna time.
The Interplay of Determinacy, Large Cardinals, and Inner Models
The standard axioms of set theory, Zermelo-Fraenkel set theory with Choice (ZFC), do not suffice to answer all questions in mathematics. While this follows abstractly from Kurt Gödel’s famous incompleteness theorems, we nowadays know numerous concrete examples for such questions. In addition to a large number of problems in set theory, even many problems outside of set theory have been showed to be unsolvable, meaning neither their truth nor their failure can be proven from ZFC. A major part of set theory is devoted to attacking this problem by studying various extensions of ZFC and their properties with the overall goal to identify the “right” axioms for mathematics that settle these problems.
Determinacy assumptions are canonical extensions of ZFC that postulate the existence of winning strategies in natural infinite two-player games. Such assumptions are known to enhance sets of real numbers with a great deal of canonical structure. Other natural and well-studied extensions of ZFC are given by the hierarchy of large cardinal axioms. Inner model theory provides canonical models for many large cardinal axioms. Determinacy assumptions, large cardinal axioms, and their consequences are widely used and have many fruitful implications in set theory and even in other areas of mathematics. Many applications, in particular, proofs of consistency strength lower bounds, exploit the interplay of determinacy axioms, large cardinals, and inner models. In this talk I will survey recent developments as well as my contribution to this flourishing area.
- 22 Jul 2021 » Winter Meeting of the ASL with the JMM - Lower bounds in set theory (cancelled)
I was invited to give an invited address at the 2022 Winter Meeting of the Association for Symbolic Logic with the JMM in Seattle, Washington, January 5-8, 2022. Due to the pandemic situation the conference is postponed and will be held as a virtual meeting later in 2022. The ASL part of the meeting is cancelled and I have been invited to speak at the 2023 JMM in Boston instead.
Lower bounds in set theory
Computing the large cardinal strength of a given statement is one of the key research directions in set theory. Fruitful tools to tackle such questions are given by inner model theory. The study of inner models was initiated by Gödel’s analysis of the constructible universe $L$. Later, it was extended to canonical inner models with large cardinals, e.g. measurable cardinals, strong cardinals or Woodin cardinals, which were introduced and studied by Jensen, Mitchell, Steel, Woodin, Sargsyan, and others.
We will outline two recent applications where inner model theory is used to obtain lower bounds in large cardinal strength for statements that do not involve inner models. The first result, joint with Y. Hayut, involves combinatorics of infinite trees and the perfect subtree property for weakly compact cardinals $\kappa$. The second result studies the strength of a model of determinacy in which all sets of reals are universally Baire. Sargsyan conjectured that the existence of such a model is as strong as the existence of a cardinal that is both a limit of Woodin cardinals and a limit of strong cardinals. Larson, Sargsyan and Wilson showed that this would be optimal via a generalization of Woodin’s derived model construction. We will discuss a new translation procedure for hybrid mice extending work of Steel, Zhu and Sargsyan and use this to prove Sargsyan’s conjecture.
- 21 Jul 2021 » Vorstellungsvortrag an der Fakultät für Mathematik und Geoinformation - The Interplay of Determinacy, Large Cardinals, and Inner Models
On November 17th, 2021, I will give a talk at the Faculty of Mathematics and Geoinformation at TU Wien. If you want to attend this zoom talk, please send me an e-mail.
The Interplay of Determinacy, Large Cardinals, and Inner Models
The standard axioms of set theory, Zermelo-Fraenkel set theory with Choice (ZFC), do not suffice to answer all questions in mathematics. While this follows abstractly from Kurt Gödel’s famous incompleteness theorems, we nowadays know numerous concrete examples for such questions. In addition to a large number of problems in set theory, even many problems outside of set theory have been showed to be unsolvable, meaning neither their truth nor their failure can be proven from ZFC. A major part of set theory is devoted to attacking this problem by studying various extensions of ZFC and their properties with the overall goal to identify the “right” axioms for mathematics that settle these problems.
Determinacy assumptions are canonical extensions of ZFC that postulate the existence of winning strategies in natural infinite two-player games. Such assumptions are known to enhance sets of real numbers with a great deal of canonical structure. Other natural and well-studied extensions of ZFC are given by the hierarchy of large cardinal axioms. Inner model theory provides canonical models for many large cardinal axioms. Determinacy assumptions, large cardinal axioms, and their consequences are widely used and have many fruitful implications in set theory and even in other areas of mathematics. Many applications, in particular, proofs of consistency strength lower bounds, exploit the interplay of determinacy axioms, large cardinals, and inner models.
In this talk I will survey my contribution to this flourishing area. This, in particular, includes results on connecting the determinacy of longer games to canonical inner models with many Woodin cardinals, a new lower bound for a combinatorial statement about infinite trees, as well as an application of determinacy answering a question in general topology.
- 20 Jul 2021 » Cross-Alps Logic Seminar - Large Cardinals and Determinacy
I am invited to give a talk on Nov 12, 2021, in the Cross-Alps Logic Seminar, an online seminar organized by the logic groups of Udine, Turin, Genoa and Lausanne.
Large Cardinals and Determinacy
Determinacy assumptions, large cardinal axioms, and their consequences are widely used and have many fruitful implications in set theory and even in other areas of mathematics. Many applications, in particular, proofs of consistency strength lower bounds, exploit the interplay of determinacy axioms, large cardinals, and inner models. I will survey some recent results in this flourishing area. This, in particular, includes results on connecting the determinacy of longer games to canonical inner models with many Woodin cardinals, a new lower bound for a combinatorial statement about infinite trees, as well as an application of determinacy answering a question in general topology.
A recording of this talk is available here.
- 20 Jul 2021 » (with C. J. Eagle, C. Hamel, and F. D. Tall) An undecidable extension of Morley's theorem on the number of countable models
- 20 Jul 2021 » DMV-ÖMG Annual Conference 2021 - Uniformization and internal absoluteness
I was invited to give a talk in the Sektion Logik at the DMV-ÖMG Annual Conference 2021 taking place virtually from Passau, Germany, Sep 27 - Oct 1, 2021.
Uniformization and internal absoluteness
Measurability with respect to ideals is known to be tightly connected to absoluteness principles for certain forcing notions. In joint work with Philipp Schlicht we study a uniformization principle that postulates the existence of a uniformizing function on a large set, relative to a given ideal. We prove that for all ideals I such that Borel/I is proper, this uniformization principle is equivalent to an absoluteness principle for projective formulas that we call internal absoluteness. In addition, we show that it is equivalent to measurability with respect to I together with 1-step absoluteness for the poset Borel/I. These equivalences are new even for Cohen and random forcing and are, to the best of our knowledge, the first precise equivalences between regularity and absoluteness beyond the second level of the projective hierarchy.
- 18 Jul 2021 » 16th International Luminy Workshop in Set Theory - The strength of determinacy when all sets are universally Baire
During the week of September 13 - 17, 2021 I virtually attended the 16th International Luminy Workshop in Set Theory and gave a talk on September 15, 2021.
The strength of determinacy when all sets are universally Baire
Abstract: The large cardinal strength of the Axiom of Determinacy when enhanced with the hypothesis that all sets of reals are universally Baire is known to be much stronger than the Axiom of Determinacy itself. In fact, Sargsyan conjectured it to be as strong as the existence of a cardinal that is both a limit of Woodin cardinals and a limit of strong cardinals. Larson, Sargsyan and Wilson showed that this would be optimal via a generalization of Woodin’s derived model construction. We will discuss a new translation procedure for hybrid mice extending work of Steel, Zhu and Sargsyan and use this to prove Sargsyan’s conjecture.
- 23 Jun 2021 » Logic Colloquium Poznan - The strength of determinacy when all sets are universally Baire
I was invited to give a talk in the special session on set theory at the Logic Colloquium 2021 taking place at the Adam Mickiewicz University, Poznan, Poland, July 19-24, 2021.
The strength of determinacy when all sets are universally Baire
The large cardinal strength of the Axiom of Determinacy when enhanced with the hypothesis that all sets of reals are universally Baire is known to be much stronger than the Axiom of Determinacy itself. In fact, Sargsyan conjectured it to be as strong as the existence of a cardinal that is both a limit of Woodin cardinals and a limit of strong cardinals. Larson, Sargsyan and Wilson showed that this would be optimal via a generalization of Woodin’s derived model construction. We will discuss a new translation procedure for hybrid mice extending work of Steel, Zhu and Sargsyan and use this to prove Sargsyan’s conjecture.
- 21 Jun 2021 » A short talk series: Research in Set Theory - Determinacy Axioms
I gave a virtual talk in the short talk series: Research in Set Theory on June 18, 2021. The talk was at 9:30pm.
Determinacy Axioms
Set theory can be understood as the search for the right axioms in mathematics, i.e., axioms that answer the questions left open by the standard axioms for set theory introduced by Zermelo and Fraenkel with the Axiom of Choice (ZFC). Canonical candidates for these axioms are large cardinals, determinacy axioms, and forcing axioms. We will focus on the second one, determinacy axioms, and say a bit about connections between large cardinals and determinacy.
A recording of this talk is available on request.
- 30 May 2021 » The consistency strength of determinacy when all sets are universally Baire
- 22 Feb 2021 » ASL North American Annual Meeting - The strength of determinacy when all sets are universally Baire
I was invited to give a talk on June 23, 2021 in the special session on set theory at the 2021 ASL North American Annual Meeting, June 22-25, 2021. This conference took place online.
The strength of determinacy when all sets are universally Baire
The large cardinal strength of the Axiom of Determinacy when enhanced with the hypothesis that all sets of reals are universally Baire is known to be much stronger than the Axiom of Determinacy itself. In fact, Sargsyan conjectured it to be as strong as the existence of a cardinal that is both a limit of Woodin cardinals and a limit of strong cardinals. Larson, Sargsyan and Wilson showed that this would be optimal via a generalization of Woodin’s derived model construction. We will discuss a new translation procedure for hybrid mice extending work of Steel, Zhu and Sargsyan and use this to prove Sargsyan’s conjecture.
- 21 Feb 2021 » Bristol/Oxford Set Theory seminar - The strength of determinacy when all sets are universally Baire
I gave a virtual talk in the Bristol/Oxford Set Theory seminar (see also) or on May 26, 2021. The talk was at 4:30pm local time, i.e., 5:30pm Vienna time.
The strength of determinacy when all sets are universally Baire
The large cardinal strength of the Axiom of Determinacy when enhanced with the hypothesis that all sets of reals are universally Baire is known to be much stronger than the Axiom of Determinacy itself. In fact, Sargsyan conjectured it to be as strong as the existence of a cardinal that is both a limit of Woodin cardinals and a limit of strong cardinals. Larson, Sargsyan and Wilson showed that this would be optimal via a generalization of Woodin’s derived model construction. We will discuss a new translation procedure for hybrid mice extending work of Steel, Zhu and Sargsyan and use this to prove Sargsyan’s conjecture.
- 20 Feb 2021 » CMU Logic Seminar, Pittsburgh - Large cardinals and determinacy when all sets are universally Baire
I am invited to give a talk in the Logic Seminar at CMU on April 20th, 2021 at 3:30pm Pittsburgh time (which is 9:30pm Vienna time). This one hour talk will be for a general audience. Afterwards I will give a 90min talk in the reading group where I will give more technical details. This seminar will take place virtually via zoom.
Large cardinals and determinacy when all sets are universally Baire
The large cardinal strength of the Axiom of Determinacy when enhanced with the hypothesis that all sets of reals are universally Baire is known to be much stronger than the Axiom of Determinacy itself. In fact, Sargsyan conjectured it to be as strong as the existence of a cardinal that is both a limit of Woodin cardinals and a limit of strong cardinals. Larson, Sargsyan and Wilson showed that this would be optimal via a generalization of Woodin’s derived model construction. After a gentle introduction to the connection between determinacy axioms and large cardinals we will sketch a proof of Sargsyan’s conjecture.
The exact consistency strength of “AD + all sets are universally Baire”
In this second talk, we will outline the proof of Sargsyan’s conjecture with more details. In particular, we will discuss a new translation procedure for hybrid mice extending work of Steel, Zhu and Sargsyan that is crucial in the construction of a model with a cardinal that is both a limit of Woodin cardinals and a limit of strong cardinals from a model of the Axiom of Determinacy in which all sets of reals are universally Baire.
- 19 Feb 2021 » CUNY Set Theory Seminar, New York - The exact consistency strength of AD + all sets are universally Baire
I am invited to give a talk in the CUNY Set Theory Seminar on April 9th, 2021. The seminar will take place via zoom.
The exact consistency strength of “AD + all sets are universally Baire”
The large cardinal strength of the Axiom of Determinacy when enhanced with the hypothesis that all sets of reals are universally Baire is known to be much stronger than the Axiom of Determinacy itself. In fact, Sargsyan conjectured it to be as strong as the existence of a cardinal that is both a limit of Woodin cardinals and a limit of strong cardinals. Larson, Sargsyan and Wilson showed that this would be optimal via a generalization of Woodin’s derived model construction. We will discuss a new translation procedure for hybrid mice extending work of Steel, Zhu and Sargsyan and use this to prove Sargsyan’s conjecture.
- 19 Feb 2021 » KGRC Research Seminar, Vienna - The exact consistency strength of $AD^+$ + all sets are universally Baire
I gave a talk in the KGRC Research Seminar at University of Vienna on Mar 11th, 2021 at 3pm Vienna time. The seminar took place via zoom.
The exact consistency strength of “$AD^+$ + all sets are universally Baire”
The large cardinal strength of the Axiom of Determinacy when enhanced with the hypothesis that all sets of reals are universally Baire is known to be much stronger than the Axiom of Determinacy itself. In fact, Sargsyan conjectured it to be as strong as the existence of a cardinal that is both a limit of Woodin cardinals and a limit of strong cardinals. Larson, Sargsyan and Wilson showed in 2014 that this would be optimal via a generalization of Woodin’s derived model construction. We will discuss a new translation procedure for hybrid mice extending work of Steel, Zhu and Sargsyan and use this to prove Sargsyan’s conjecture.
- 16 Jan 2021 » IMU DMV meeting Jerusalem - Cancelled
I was invited to give a talk in the special session on set theory at the joint meeting of the Israeli Mathematical Union (IMU) and the German Mathematical Society (DMV) that was supposed to take place at the Hebrew University, Jerusalem, Israel, Mar 08-10, 2021.
This meeting got cancelled due to the ongoing Covid-19 pandemic.
- 15 Jan 2021 » World Logic Day, Hamburg - Unendliche Spiele und die Grenzen der Mathematik
I was invited to give a talk for a general audience at the celebration of the World Logic Day taking place virtually in Hamburg, Germany on January 15, 2021. This talk was in German.
Unendliche Spiele und die Grenzen der Mathematik
- 27 Nov 2020 » Set Theory Seminar, The Fields Institute, Toronto - The Large Cardinal Strength of Determinacy Axioms
I gave a talk in the Set Theory Seminar at the Fields Institute in Toronto on Nov 27th, 2020 at 1:30pm Toronto time (which is 7:30pm Vienna time). This seminar took place virtually via zoom.
The Large Cardinal Strength of Determinacy Axioms
Abstract: The study of inner models was initiated by Gödel’s analysis of the constructible universe $L$. Later, it became necessary to study canonical inner models with large cardinals, e.g. measurable cardinals, strong cardinals or Woodin cardinals, which were introduced by Jensen, Mitchell, Steel, and others. Around the same time, the study of infinite two-player games was driven forward by Martin’s proof of analytic determinacy from a measurable cardinal, Borel determinacy from ZFC, and Martin and Steel’s proof of levels of projective determinacy from Woodin cardinals with a measurable cardinal on top. First Woodin and later Neeman improved the result in the projective hierarchy by showing that in fact the existence of a countable iterable model, a mouse, with Woodin cardinals and a top measure suffices to prove determinacy in the projective hierarchy.
This opened up the possibility for an optimal result stating the equivalence between local determinacy hypotheses and the existence of mice in the projective hierarchy, just like the equivalence of analytic determinacy and the existence of $x^\sharp$ for every real $x$ which was shown by Martin and Harrington in the 70’s. The existence of mice with Woodin cardinals and a top measure from levels of projective determinacy was shown by Woodin in the 90’s. Together with his earlier and Neeman’s results this estabilishes a tight connection between descriptive set theory in the projective hierarchy and inner model theory.
In this talk, we will outline some of the main results connecting determinacy hypotheses with the existence of mice with large cardinals and discuss a number of more recent results in this area.
- 05 Nov 2020 » Ghent–Leeds Virtual Logic Seminar - Determinacy and inner models
I gave a talk in the Ghent–Leeds Virtual Logic Seminar on Nov 05, 2020. This seminar took place virtually via zoom.
Determinacy and inner models
Abstract: The study of inner models was initiated by Gödel’s analysis of the constructible universe $L$. Later, it became necessary to study canonical inner models with large cardinals, e.g. measurable cardinals, strong cardinals or Woodin cardinals, which were introduced by Jensen, Mitchell, Steel, and others. Around the same time, the study of infinite two-player games was driven forward by Martin’s proof of analytic determinacy from a measurable cardinal, Borel determinacy from ZFC, and Martin and Steel’s proof of levels of projective determinacy from Woodin cardinals with a measurable cardinal on top. First Woodin and later Neeman improved the result in the projective hierarchy by showing that in fact the existence of a countable iterable model, a mouse, with Woodin cardinals and a top measure suffices to prove determinacy in the projective hierarchy.
This opened up the possibility for an optimal result stating the equivalence between local determinacy hypotheses and the existence of mice in the projective hierarchy, just like the equivalence of analytic determinacy and the existence of $x^\sharp$ for every real $x$ which was shown by Martin and Harrington in the 70’s. The existence of mice with Woodin cardinals and a top measure from levels of projective determinacy was shown by Woodin in the 90’s. Together with his earlier and Neeman’s results this estabilishes a tight connection between descriptive set theory in the projective hierarchy and inner model theory.
In this talk, we will outline some of the main results connecting determinacy hypotheses with the existence of mice with large cardinals and discuss a number of more recent results in this area, some of which are joint work with Juan Aguilera.
- 29 Sep 2020 » (with P. Lücke) Closure properties of measurable ultrapowers
The Journal of Symbolic Logic. Volume 86, Issue 2, June 2021. Pages 762-784.
DOI: 10.1017/jsl.2021.29. PDF. arXiv. Bibtex. - 08 May 2020 » CUNY Set Theory Seminar, New York - How to obtain lower bounds in set theory
I gave a talk in the CUNY Set Theory Seminar at CUNY, New York, on May 08, 2020. This seminar took place virtually via zoom.
How to obtain lower bounds in set theory
Abstract: Computing the large cardinal strength of a given statement is one of the key research directions in set theory. Fruitful tools to tackle such questions are given by inner model theory. The study of inner models was initiated by Gödel’s analysis of the constructible universe $L$. Later, it was extended to canonical inner models with large cardinals, e.g. measurable cardinals, strong cardinals or Woodin cardinals, which were introduced by Jensen, Mitchell, Steel, and others.
We will outline two recent applications where inner model theory is used to obtain lower bounds in large cardinal strength for statements that do not involve inner models. The first result, in part joint with J. Aguilera, is an analysis of the strength of determinacy for certain infinite two player games of fixed countable length, and the second result, joint with Y. Hayut, involves combinatorics of infinite trees and the perfect subtree property for weakly compact cardinals $\kappa$. Finally, we will comment on obstacles, questions, and conjectures for lifting these results higher up in the large cardinal hierarchy.
- 30 Apr 2020 » Research Seminar, Vienna - How to obtain lower bounds in set theory
I gave a talk in the Research Seminar at the University of Vienna on April 30, 2020. This seminar took place virtually via zoom.
How to obtain lower bounds in set theory
Abstract: Computing the large cardinal strength of a given statement is one of the key research directions in set theory. Fruitful tools to tackle such questions are given by inner model theory. The study of inner models was initiated by Gödel’s analysis of the constructible universe $L$. Later, it was extended to canonical inner models with large cardinals, e.g. measurable cardinals, strong cardinals or Woodin cardinals, which were introduced by Jensen, Mitchell, Steel, and others.
We will outline two recent applications where inner model theory is used to obtain lower bounds in large cardinal strength for statements that do not involve inner models. The first result, in part joint with J. Aguilera, is an analysis of the strength of determinacy for certain infinite two player games of fixed countable length, and the second result, joint with Y. Hayut, involves combinatorics of infinite trees and the perfect subtree property for weakly compact cardinals $\kappa$.
- 06 Mar 2020 » Consistency strength lower bounds for the proper forcing axiom via the core model induction
Bulletin of Symbolic Logic. Volume 26, Issue 1, December 2020. Pages 89-92.
DOI: 10.1017/bsl.2020.6. PDF. Bibtex. - 05 Mar 2020 » North American Annual Meeting of the ASL - How to obtain lower bounds in set theory
I was invited to give a plenary talk at the 2020 North American Annual Meeting of the Association for Symbolic Logic taking place at UC Irvine March 25-28, 2020. Due to the public health concerns over COVID-19, this meeting was cancelled and instead held as a virtual meeting.
How to obtain lower bounds in set theory
Computing the large cardinal strength of a given statement is one of the key research directions in set theory. Fruitful tools to tackle such questions are given by inner model theory. The study of inner models was initiated by Gödel’s analysis of the constructible universe $L$. Later, it was extended to canonical inner models with large cardinals, e.g. measurable cardinals, strong cardinals or Woodin cardinals, which were introduced by Jensen, Mitchell, Steel, and others.
We will outline three recent applications where inner model theory is used to obtain lower bounds in large cardinal strength for statements that do not involve inner models. The first result, in part joint with J. Aguilera, is an analysis of the strength of determinacy for certain infinite two player games of fixed countable length, the second result studies the strength of a model of determinacy in which all sets of reals are universally Baire, and the third result, joint with Y. Hayut, involves combinatorics of infinite trees and the perfect subtree property for weakly compact cardinals $\kappa$.
- 04 Mar 2020 » International Day of Mathematics, Vienna - Das Unbegreifliche verstehen - die Faszination Unendlichkeit
I am invited to give a talk for a general audience at the celebration of the International Day of Mathematics taking place at the TU Wien on March 14, 2020. This talk will be in German.
This meeting was cancelled due to the COVID-19 restrictions.
Das Unbegreifliche verstehen - die Faszination Unendlichkeit
Jeder kennt sie, sie ist immer da, aber nie so richtig - die Unendlichkeit. Aber was meinen wir eigentlich, wenn wir sagen, dass etwas unendlich groß ist? Gibt es nur die eine Unendlichkeit oder zwei oder vielleicht sogar ganz viele?
Wir werden diese Fragen und natürlich auch die dazugehörigen Antworten etwas genauer unter die Lupe nehmen. Dabei wird sich nicht nur zeigen, wozu Mathematik in der Lage ist, sondern wir werden uns auch auf den Weg zu den Grenzen der Mathematik machen, wie sie zum Beispiel von Cantor und Gödel aufgezeigt wurden. Diese Grenzen besser zu verstehen - getreu nach dem Spruch von Oliver Tietze „Wer mit dem Feuer spielen will, muss wissen, wo das Wasser steht.“ - ist noch heute Gegenstand mathematischer Spitzenforschung.
- 19 Nov 2019 » Oberseminar mathematische Logik, Bonn - Infinite decreasing chains in the Mitchell order
I gave a talk in the Oberseminar mathematische Logik at the University of Bonn on January 14, 2020.
Infinite decreasing chains in the Mitchell order
Abstract: It is known that the behavior of the Mitchell order substantially changes at the level of rank-to-rank extenders, as it ceases to be well-founded. While the possible partial order structure of the Mitchell order below rank-to-rank extenders is considered to be well understood, little is known about the structure in the ill-founded case. We make a first step in understanding this case by studying the extent to which the Mitchell order can be ill-founded. Our main results are (i) in the presence of a rank-to-rank extender there is a transitive Mitchell order decreasing sequence of extenders of any countable length, and (ii) there is no such sequence of length $\omega_1$. This is joint work with Omer Ben-Neria.
As this is a blackboard talk there are no slides available, you can find a preprint related to this talk here.
- 05 Oct 2019 » (with S.-D. Friedman and V. Gitman) Structural Properties of the Stable Core
Accepted for publication in the Journal of Symbolic Logic. PDF. arXiv. Bibtex.
- 28 Aug 2019 » CUNY Logic Workshop - Infinite decreasing chains in the Mitchell order
I was invited to give a talk in the CUNY Logic Workshop on Nov 15, 2019.
Infinite decreasing chains in the Mitchell order
Abstract: It is known that the behavior of the Mitchell order substantially changes at the level of rank-to-rank extenders, as it ceases to be well-founded. While the possible partial order structure of the Mitchell order below rank-to-rank extenders is considered to be well understood, little is known about the structure in the ill-founded case. We make a first step in understanding this case by studying the extent to which the Mitchell order can be ill-founded. Our main results are (i) in the presence of a rank-to-rank extender there is a transitive Mitchell order decreasing sequence of extenders of any countable length, and (ii) there is no such sequence of length $\omega_1$. This is joint work with Omer Ben-Neria.
As this is a blackboard talk there are no slides available, you can find a preprint related to this talk here.
- 28 Aug 2019 » (with O. Ben-Neria) Infinite decreasing chains in the Mitchell order
Archive for Mathematical Logic. Volume 60, March 2021. Pages 771-781.
DOI: 10.1007/s00153-021-00762-x. PDF. arXiv. Bibtex. - 15 Jul 2019 » Rutgers MAMLS 2019 - Sealed Trees and the Perfect Subtree Property for Weakly Compact Cardinals
I was invited to give a talk at the 2019 edition of Rutgers MAMLS taking place Nov 1-3, 2019 at Rutgers University, USA.
Sealed Trees and the Perfect Subtree Property for Weakly Compact Cardinals
Abstract: We investigate the consistency strength of the statement: $\kappa$ is weakly compact and there is no tree on $\kappa$ with exactly $\kappa^{+}$ many branches. We show that this property fails strongly (there is a sealed tree) if there is no inner model with a Woodin cardinal. On the other hand, we show that this property as well as the related Perfect Subtree Property for $\kappa$, implies the consistency of $\operatorname{AD}_{\mathbb{R}}$. This is joint work with Yair Hayut.
- 14 Jul 2019 » 15th International Luminy Workshop in Set Theory - Lower bounds for the perfect subtree property at weakly compact cardinals
During the week of September 23 - 27, 2019 I attended the 15th International Luminy Workshop in Set Theory and gave a talk.
Lower bounds for the perfect subtree property at weakly compact cardinals
Abstract: By the Cantor-Bendixson theorem, subtrees of the binary tree on $\omega$ satisfy a dichotomy - either the tree has countably many branches or there is a perfect subtree (and in particular, the tree has continuum many branches, regardless of the size of the continuum). We generalize this to arbitrary regular cardinals $\kappa$ and ask whether every $\kappa$-tree with more than $\kappa$ branches has a perfect subtree. From large cardinals, this statement is consistent at a weakly compact cardinal $\kappa$. We show using stacking mice that the existence of a non-domestic mouse (which yields a model with a proper class of Woodin cardinals and strong cardinals) is a lower bound. Moreover, we study variants of this statement involving sealed trees, i.e. trees with the property that their set of branches cannot be changed by certain forcings, and obtain lower bounds for these as well. This is joint work with Yair Hayut.
Click here to go to the video in the CIRM library.
- 12 Jul 2019 » (with R. Carroy and A. Medini) Constructing Wadge classes
Accepted for publication in the Bulletin of Symbolic Logic. PDF. arXiv. Bibtex.
- 08 Jul 2019 » (with J. Aguilera) Projective Games on the Reals
Notre Dame Journal of Formal Logic. Volume 61, Issue 4, November 2020. Pages 573-589.
DOI: 10.1215/00294527-2020-0027. PDF. arXiv. Bibtex. - 01 Mar 2019 » (with Niklas Mueller, Joachim Streis, Hermann Pavenstädt, Thomas Felderhoff, Stefan Reuter und Veit Busch) Pulse Wave Analysis and Pulse Wave Velocity for Fistula Assessment
Kidney & Blood Pressure Research. Volume 45, Issue 4, July 2020. Pages 576-588.
DOI: 10.1159/000506741. PDF. Bibtex. - 09 Feb 2019 » The Core Model Induction and Other Inner Model Theoretic Tools Rutgers - Tutorial: HOD Computations
As a part of the workshop on “The Core Model Induction and Other Inner Model Theoretic Tools” in Rutgers I gave a tutorial on HOD Computations.
Abstract: An essential question regarding the theory of inner models is the analysis of the class of all hereditarily ordinal definable sets HOD inside various inner models $M$ of the set theoretic universe $V$ under appropriate determinacy hypotheses. Examples for such inner models $M$ are $L(\mathbb{R})$ or $L[x]$ on a cone of reals $x$. We will outline Steel’s and Woodin’s analysis of $HOD^{L(\mathbb{R})}$. Moreover, we will discuss their analysis of $HOD^{L[x,G]}$ on a cone of reals $x$, where $G$ is $Col(\omega,\kappa)$-generic and $\kappa$ is the least inaccessible cardinal in $L[x]$. We will point out were the problems are when trying to adapt this to analyze $HOD^{L[x]}$.
Reading List:
- (Steel) An outline of inner model theory, Handbook of Set Theory, Section 8.
- (Steel, Woodin) HOD as a core model, Cabal III.
Necessary requirements:
A good understanding of mice, the comparison process and genericity iterations, e.g. the fine structure tutorial given in the first week or the relevant parts of Steel’s handbook chapter (Sections 1-3 and 7).
See here for more information about the meeting and here for lecture notes typed by James Holland.
- 08 Feb 2019 » Logic Fest in the Windy City - The interplay between inner model theory and descriptive set theory in a nutshell
On June 01, 2019 I was invited to give a talk at the Logic Fest in the Windy City in Chicago, USA.
The interplay between inner model theory and descriptive set theory in a nutshell
Abstract: The study of inner models was initiated by Gödel’s analysis of the constructible universe $L$. Later, it became necessary to study canonical inner models with large cardinals, e.g. measurable cardinals, strong cardinals or Woodin cardinals, which were introduced by Jensen, Mitchell, Steel, and others. Around the same time, the study of infinite two-player games was driven forward by Martin’s proof of analytic determinacy from a measurable cardinal, Borel determinacy from ZFC, and Martin and Steel’s proof of levels of projective determinacy from Woodin cardinals with a measurable cardinal on top. First Woodin and later Neeman improved the result in the projective hierarchy by showing that in fact the existence of a countable iterable model, a mouse, with Woodin cardinals and a top measure suffices to prove determinacy in the projective hierarchy.
This opened up the possibility for an optimal result stating the equivalence between local determinacy hypotheses and the existence of mice in the projective hierarchy, just like the equivalence of analytic determinacy and the existence of $x^\sharp$ for every real $x$ which was shown by Martin and Harrington in the 70’s. The existence of mice with Woodin cardinals and a top measure from levels of projective determinacy was shown by Woodin in the 90’s. Together with his earlier and Neeman’s results this estabilishes a tight connection between descriptive set theory in the projective hierarchy and inner model theory.
In this talk, we will outline the main concepts and results connecting determinacy hypotheses with the existence of mice with large cardinals. Neeman’s methods mentioned above extend to show determinacy of projective games of arbitrary countable length from the existence of inner models with many Woodin cardinals. We will discuss a number of more recent results, some of which are joint work with Juan Aguilera, showing that inner models with many Woodin cardinals can be obtained from the determinacy of countable projective games.
- 25 Jan 2019 » Set Theory Seminar Bar-Ilan University - Projective determinacy for games of length omega^2 and longer
On February 25, 2019 I was invited to give a talk in the Set Theory Seminar at Bar-Ilan University, Israel.
Projective determinacy for games of length $\omega^2$ and longer
Abstract: We will study infinite two player games and the large cardinal strength corresponding to their determinacy. For games of length $\omega$ this is well understood and there is a tight connection between the determinacy of projective games and the existence of canonical inner models with Woodin cardinals. For games of arbitrary countable length, Itay Neeman proved the determinacy of analytic games of length $\omega \cdot \theta$ for countable $\theta > \omega$ from a sharp for $\theta$ Woodin cardinals.
We aim for a converse at successor ordinals. In joint work with Juan P. Aguilera we showed that determinacy of $\boldsymbol\Pi^1_{n+1}$ games of length $\omega^2$ implies the existence of a premouse with $\omega+n$ Woodin cardinals. This generalizes to a premouse with $\omega+\omega$ Woodin cardinals from the determinacy of games of length $\omega^2$ with $\Game^{\mathbb{R}}\boldsymbol\Pi^1_1$ payoff.
If time allows, we will also sketch how these methods can be adapted to, in combination with results of Nam Trang, obtain $\omega^\alpha+n$ Woodin cardinals for countable ordinals $\alpha$ and natural numbers $n$ from the determinacy of sufficiently long projective games.
- 07 Nov 2018 » Logic and Set Theory Seminar Bristol - The consistency strength of long projective determinacy
On February 05, 2019 I was invited to give a talk in the Logic and Set Theory Seminar in Bristol.
The consistency strength of long projective determinacy
Abstract: We will study infinite two player games and the large cardinal strength corresponding to their determinacy. For games of length $\omega$ this is well understood and there is a tight connection between the determinacy of projective games and the existence of canonical inner models with Woodin cardinals. For games of arbitrary countable length, Itay Neeman proved the determinacy of analytic games of length $\omega \cdot \theta$ for countable $\theta > \omega$ from a sharp for $\theta$ Woodin cardinals.
We aim for a converse at successor ordinals. In joint work with Juan P. Aguilera we showed that determinacy of $\boldsymbol\Pi^1_{n+1}$ games of length $\omega^2$ implies the existence of a premouse with $\omega+n$ Woodin cardinals. This generalizes to a premouse with $\omega+\omega$ Woodin cardinals from the determinacy of games of length $\omega^2$ with $\Game^{\mathbb{R}}\boldsymbol\Pi^1_1$ payoff.
If time allows, we will also sketch how these methods can be adapted to, in combination with results of Nam Trang, obtain $\omega^\alpha+n$ Woodin cardinals for countable ordinals $\alpha$ and natural numbers $n$ from the determinacy of sufficiently long projective games.
- 07 Nov 2018 » (with J. Aguilera) The consistency strength of long projective determinacy
The Journal of Symbolic Logic. Volume 85, Issue 1, March 2020. Pages 338-366.
DOI: 10.1017/jsl.2019.78. PDF. arXiv. Bibtex. - 06 Nov 2018 » Arctic Set Theory Workshop 4 - Homogeneous Spaces and Wadge Theory
On January 22, 2019 I gave a talk at the (Arctic Set Theory Workshop 4) in Kilpisjärvi, Finland.
Homogeneous Spaces and Wadge Theory
Abstract: In his PhD thesis Wadge characterized the notion of continuous reducibility on the Baire space ${}^\omega\omega$ in form of a game and analyzed it in a systematic way. He defined a refinement of the Borel hierarchy, called the Wadge hierarchy, showed that it is well-founded, and (assuming determinacy for Borel sets) proved that every Borel pointclass appears in this classification. Later Louveau found a description of all levels in the Borel Wadge hierarchy using Boolean operations on sets. Fons van Engelen used this description to analyze Borel homogeneous spaces and show that every homogeneous Borel space is in fact strongly homogeneous.
In this talk, we will show how to generalize these results under the Axiom of Determinacy. In particular, we will outline that under AD every homogeneous space is in fact strongly homogeneous.
This is joint work with Raphaël Carroy and Andrea Medini.
Slides can be found here.
- 06 Nov 2018 » The Axiom of Determinacy implies Dependent Choice in mice
Mathematical Logic Quarterly. Volume 65, Issue 3, October 2019. Pages 370-375.
DOI: 10.1002/malq.201800077. PDF. arXiv. Bibtex. - 05 Nov 2018 » Rutgers Logic Seminar - The consistency strength of long projective determinacy
On December 10, 2018 I gave a talk in the Rutgers Logic Seminar.
The consistency strength of long projective determinacy
Abstract: We will study infinite two player games and the large cardinal strength corresponding to their determinacy. For games of length $\omega$ this is well understood and there is a tight connection between the determinacy of projective games and the existence of canonical inner models with Woodin cardinals. For games of arbitrary countable length, Itay Neeman proved the determinacy of analytic games of length $\omega \cdot \theta$ for countable $\theta > \omega$ from a sharp for $\theta$ Woodin cardinals.
We aim for a converse at successor ordinals. In joint work with Juan P. Aguilera we showed that determinacy of $\boldsymbol\Pi^1_{n+1}$ games of length $\omega^2$ implies the existence of a premouse with $\omega+n$ Woodin cardinals. This generalizes to a premouse with $\omega+\omega$ Woodin cardinals from the determinacy of games of length $\omega^2$ with $\Game^{\mathbb{R}}\boldsymbol\Pi^1_1$ payoff.
If time allows, we will also sketch how these methods can be adapted to obtain for example $\omega^2+n$ Woodin cardinals from the determinacy of sufficiently long projective games.
- 04 Nov 2018 » Oberseminar mathematische Logik Bonn - Structural properties of the Stable Core
On December 04, 2018 I gave a talk in the Oberseminar mathematische Logik in Bonn.
Structural properties of the Stable Core
Abstract: The Stable Core $\mathbb{S}$, introduced by Sy Friedman in 2012, is a proper class model of the form $(L[S],S)$ for a simply definable predicate $S$. He showed that $V$ is generic over the Stable Core (for $\mathbb{S}$-definable dense classes) and that the Stable Core can be properly contained in HOD. These remarkable results motivate the study of the Stable Core itself. In the light of other canonical inner models the questions whether the Stable Core satisfies GCH or whether large cardinals is $V$ imply their existence in the Stable Core naturally arise.
In a joint work with Sy Friedman and Victoria Gitman we give some answers to these questions and show that GCH can fail at all regular cardinals in the Stable Core. Moreover, we show that measurable cardinals in general need not be downward absolute to the Stable Core, but in the special case where $V = L[\mu]$ is the canonical inner model for one measurable cardinal, the Stable Core is in fact equal to $L[\mu]$.
- 01 Sep 2018 » (with J. Aguilera and P. Schlicht) Long games and sigma-projective sets
Annals of Pure and Applied Logic. Volume 172, Issue 4, April 2021. 102939.
DOI: 10.1016/j.apal.2020.102939. PDF. arXiv. Bibtex. - 21 Aug 2018 » UMI-SIMAI-PTM, Wroclaw - Large Cardinals in the Stable Core
On September 19, 2018 I was invited to give a talk in the Thematic Session in Set Theory and Topology at the joint meeting of the Italian Mathematical Union, the Italian Society of Industrial and Applied Mathematics and the Polish Mathematical Society (UMI-SIMAI-PTM) in Wrocław.
Large Cardinals in the Stable Core
Abstract: The Stable Core $\mathbb{S}$, introduced by Sy Friedman in 2012, is a proper class model of the form $(L[S],S)$ for a simply definable predicate $S$. He showed that $V$ is generic over the Stable Core (for $\mathbb{S}$-definable dense classes) and that the Stable Core can be properly contained in HOD. These remarkable results motivate the study of the Stable Core itself. In the light of other canonical inner models the questions whether the Stable Core satisfies GCH or whether large cardinals is $V$ imply their existence in the Stable Core naturally arise. We answer these questions and show that GCH can fail at all regular cardinals in the Stable Core. Moreover, we show that measurable cardinals in general need not be downward absolute to the Stable Core, but in the special case where $V = L[\mu]$ is the canonical inner model for one measurable cardinal, the Stable Core is in fact equal to $L[\mu]$.
This is joint work with Sy Friedman and Victoria Gitman.
Slides for this talk are available on request.
- 20 Aug 2018 » CUNY Set Theory Seminar - How to obtain Woodin cardinals from the determinacy of long games
On September 7, 2018 I gave a talk in the CUNY Set Theory Seminar in New York.
How to obtain Woodin cardinals from the determinacy of long games
Abstract: We will study infinite two player games and the large cardinal strength corresponding to their determinacy. For games of length $\omega$ this is well understood and there is a tight connection between the determinacy of projective games and the existence of canonical inner models with Woodin cardinals. For games of arbitrary countable length, Itay Neeman proved the determinacy of analytic games of length $\omega \cdot \theta$ for countable $\theta > \omega$ from a sharp for $\theta$ Woodin cardinals. We aim for a converse at successor ordinals and sketch how to obtain $\omega+n$ Woodin cardinals from the determinacy of $\boldsymbol\Pi^1_{n+1}$ games of length $\omega^2$. Moreover, we outline how to generalize this to construct a model with $\omega+\omega$ Woodin cardinals from the determinacy games of length $\omega^2$ with $\Game^{\mathbb{R}}\boldsymbol\Pi^1_1$ payoff.
This is joint work with Juan P. Aguilera.
- 08 Jun 2018 » KNAW Academy Colloquium on Generalised Baire Spaces - Lebesgue's Density Theorem for tree forcing ideals
On August 24th, 2018 I gave a short talk at the KNAW Academy Colloquium on Generalised Baire Spaces taking place August 23rd and 24th in Amsterdam, The Netherlands.
Abstract: Lebesgue introduced a notion of density point of a set of reals and proved that any Borel set of reals has the density property, i.e. it is equal to the set of its density points up to a null set. We introduce alternative definitions of density points in Cantor space (or Baire space) which coincide with the usual definition of density points for the uniform measure on ${}^{\omega}2$ up to a set of measure $0$, and which depend only on the ideal of measure $0$ sets but not on the measure itself. This allows us to define the density property for the ideals associated to tree forcings analogous to the Lebesgue density theorem for the uniform measure on ${}^{\omega}2$. The main results show that among the ideals associated to well-known tree forcings, the density property holds for all such ccc forcings and fails for the remaining forcings. In fact we introduce the notion of being stem-linked and show that every stem-linked tree forcing has the density property.
This is joint work with Philipp Schlicht, David Schrittesser and Thilo Weinert.
Slides are available here.
- 07 Jun 2018 » 1st Girona conference on inner model theory - Long games and Woodin cardinals
On July 17, 2018 I gave a talk at the 1st Girona conference on inner model theory in Girona.
Long games and Woodin cardinals
Abstract: Itay Neeman proved the determinacy of analytic games of length $\omega \cdot \theta$ for countable $\theta > \omega$ from a sharp for $\theta$ Woodin cardinals. We aim for a converse at successor ordinals and show how to obtain $\omega+1$ Woodin cardinals from the determinacy of analytic games of length $\omega \cdot (\omega+1)$.
This is joint work with Juan P. Aguilera.
Notes for this talk are available here.
- 01 Jun 2018 » (with R. Carroy and A. Medini) Every zero-dimensional homogeneous space is strongly homogeneous under determinacy
Journal of Mathematical Logic. Volume 20, Issue 3, March 2020. 2050015.
DOI: 10.1142/S0219061320500154. PDF. arXiv. Bibtex. - 22 Mar 2018 » Oberseminar Konstanz - Large cardinals from the determinacy of games
On July 9th, 2018 I gave a 90min talk in the Oberseminar Mathematical Logic at the University of Konstanz, Germany.
Large cardinals from the determinacy of games
Abstract: We will study infinite two player games and the large cardinal strength corresponding to their determinacy. In particular, we will consider mice, which are sufficiently iterable models of set theory, and outline how they play an important role in measuring the exact strength of determinacy hypotheses. After summarizing the situation within the projective hierarchy for games of length $\omega$, we will go beyond that and consider the determinacy of even longer games. In particular, we will sketch the argument that determinacy of analytic games of length $\omega \cdot (\omega+1)$ implies the consistency of $\omega+1$ Woodin cardinals. This part is joint work with Juan P. Aguilera.
- 15 Mar 2018 » Turin - Combinatorial Variants of Lebesgue's Density Theorem
In the first week of April 2018 I will visited the Mathematical Logic group of Turin and gave a 2h talk on April 6.
Abstract: Lebesgue introduced a notion of density point of a set of reals and proved that any Borel set of reals has the density property, i.e. it is equal to the set of its density points up to a null set. We introduce alternative definitions of density points in Cantor space (or Baire space) which coincide with the usual definition of density points for the uniform measure on ${}^{\omega}2$ up to a set of measure $0$, and which depend only on the ideal of measure $0$ sets but not on the measure itself. This allows us to define the density property for the ideals associated to tree forcings analogous to the Lebesgue density theorem for the uniform measure on ${}^{\omega}2$. The main results show that among the ideals associated to well-known tree forcings, the density property holds for all such ccc forcings and fails for the remaining forcings. In fact we introduce the notion of being stem-linked and show that every stem-linked tree forcing has the density property.
This is joint work with Philipp Schlicht, David Schrittesser and Thilo Weinert.
Slides are available on request.
- 06 Mar 2018 » GDMV Jahrestagung Paderborn - Projective homogeneous spaces and the Wadge hierarchy
On March 06, 2018 I gave an invited talk in the Section in Logic at the annual meeting GDMV of the German Mathematical Society (DMV) joint with GDM taking place March 5th to 9th in Paderborn, Germany.
Abstract: In his PhD thesis Wadge characterized the notion of continuous reducibility on the Baire space ${}^\omega\omega$ in form of a game and analyzed it in a systematic way. He defined a refinement of the Borel hierarchy, called the Wadge hierarchy, showed that it is well-founded, and (assuming determinacy for Borel sets) proved that every Borel pointclass appears in this classification. Later Louveau found a description of all levels in the Borel Wadge hierarchy using Boolean operations on sets. Fons van Engelen used this description to analyze Borel homogeneous spaces.
In this talk, we will discuss the basics behind these results and show the first steps towards generalizing them to the projective hierarchy, assuming projective determinacy (PD). In particular, we will outline that under PD every homogeneous projective space is in fact strongly homogeneous.
This is joint work with Raphaël Carroy and Andrea Medini.
- 01 Dec 2017 » CUNY Set Theory Seminar - Canonical inner models and their HODs
On Dec 1st, 2017, at 10:00am I gave a talk in the CUNY Set Theory Seminar.
Abstract: An essential question regarding the theory of inner models is the analysis of the class of all hereditarily ordinal definable sets $\operatorname{HOD}$ inside various inner models $M$ of the set theoretic universe $V$ under appropriate determinacy hypotheses. Examples for such inner models $M$ are $L(\mathbb{R})$, $L[x]$ and $M_n(x)$. Woodin showed that under determinacy hypotheses these models of the form $\operatorname{HOD}^M$ contain large cardinals, which motivates the question whether they are fine-structural as for example the models $L(\mathbb{R})$, $L[x]$ and $M_n(x)$ are. A positive answer to this question would yield that they are models of $\operatorname{CH}, \Diamond$, and other combinatorial principles.
The first model which was analyzed in this sense was $\operatorname{HOD}^{L(\mathbb{R})}$ under the assumption that every set of reals in $L(\mathbb{R})$ is determined. In the 1990’s Steel and Woodin were able to show that $\operatorname{HOD}^{L(\mathbb{R})} = L[M_\infty, \Lambda]$, where $M_\infty$ is a direct limit of iterates of the canonical mouse $M_\omega$ and $\Lambda$ is a partial iteration strategy for $M_\infty$. Moreover Woodin obtained a similar result for the model $\operatorname{HOD}^{L[x,G]}$ assuming $\Delta^1_2$ determinacy, where $x$ is a real of sufficiently high Turing degree, $G$ is $\operatorname{Col}(\omega, {<}\kappa_x)$-generic over $L[x]$ and $\kappa_x$ is the least inaccessible cardinal in $L[x]$.
In this talk I will give an overview of these results (including some background on inner model theory) and outline how they can be extended to the model $\operatorname{HOD}^{M_n(x,g)}$ assuming $\boldsymbol\Pi^1_{n+2}$ determinacy, where $x$ again is a real of sufficiently high Turing degree, $g$ is $\operatorname{Col}(\omega, {<}\kappa_x)$-generic over $M_n(x)$ and $\kappa_x$ is the least inaccessible cardinal in $M_n(x)$.
This is joint work with Grigor Sargsyan.
- 14 Aug 2017 » Logic Colloquium Stockholm - The hereditarily ordinal definable sets in inner models with finitely many Woodin cardinals
On August 14th, 2017 I gave a talk in the special session on set theory at the Logic Colloquium 2017 (August 14-20, 2017).
Abstract: An essential question regarding the theory of inner models is the analysis of the class of all hereditarily ordinal definable sets $\operatorname{HOD}$ inside various inner models $M$ of the set theoretic universe $V$ under appropriate determinacy hypotheses. Examples for such inner models $M$ are $L(\mathbb{R})$, $L[x]$ and $M_n(x)$. Woodin showed that under determinacy hypotheses these models of the form $\operatorname{HOD}^M$ contain large cardinals, which motivates the question whether they are fine-structural as for example the models $L(\mathbb{R})$, $L[x]$ and $M_n(x)$ are. A positive answer to this question would yield that they are models of $\operatorname{CH}, \Diamond$, and other combinatorial principles.
The first model which was analyzed in this sense was $\operatorname{HOD}^{L(\mathbb{R})}$ under the assumption that every set of reals in $L(\mathbb{R})$ is determined. In the 1990’s Steel and Woodin were able to show that $\operatorname{HOD}^{L(\mathbb{R})} = L[M_\infty, \Lambda]$, where $M_\infty$ is a direct limit of iterates of the canonical mouse $M_\omega$ and $\Lambda$ is a partial iteration strategy for $M_\infty$. Moreover Woodin obtained a similar result for the model $\operatorname{HOD}^{L[x,G]}$ assuming $\Delta^1_2$ determinacy, where $x$ is a real of sufficiently high Turing degree, $G$ is $\operatorname{Col}(\omega, {<}\kappa_x)$-generic over $L[x]$ and $\kappa_x$ is the least inaccessible cardinal in $L[x]$.
In this talk I will give an overview of these results and outline how they can be extended to the model $\operatorname{HOD}^{M_n(x,g)}$ assuming $\boldsymbol\Pi^1_{n+2}$ determinacy, where $x$ again is a real of sufficiently high Turing degree, $g$ is $\operatorname{Col}(\omega, {<}\kappa_x)$-generic over $M_n(x)$ and $\kappa_x$ is the least inaccessible cutpoint in $M_n(x)$ which is a limit of cutpoints in $M_n(x)$.
This is joint work with Grigor Sargsyan.
This abstract will be published in the Bulletin of Symbolic Logic (BSL). My slides can be found here. A preprint containing these results will be uploaded on my webpage soon.
- 25 Jul 2017 » Münster conference on inner model theory - HOD in inner models with Woodin cardinals
On July 25th I gave a talk at the 4th Münster conference on inner model theory.
Abstract: We analyze $\operatorname{HOD}$ in the inner model $M_n(x,g)$ for reals $x$ of sufficiently high Turing degree and suitable generics $g$. Our analysis generalizes to other canonical minimal mice with Woodin and strong cardinals. This is joint work with Grigor Sargsyan.
Notes taken by Ralf Schindler during my talk can be found here. These notes include a sketch of the proof of our main result, the corresponding preprint will be uploaded on my webpage soon.
- 03 Jul 2017 » European Set Theory Conference - Combinatorial Variants of Lebesgue's Density Theorem
On July 3rd 2017 I gave a contributed talk at the 6th European Set Theory Conference in Budapest.
Abstract: We introduce alternative definitions of density points in Cantor space (or Baire space) which coincide with the usual definition of density points for the uniform measure on ${}^{\omega}2$ up to a set of measure $0$, and which depend only on the ideal of measure $0$ sets but not on the measure itself. This allows us to define the density property for the ideals associated to tree forcings analogous to the Lebesgue density theorem for the uniform measure on ${}^{\omega}2$. The main results show that among the ideals associated to well-known tree forcings, the density property holds for all such ccc forcings and fails for the remaining forcings. In fact we introduce the notion of being stem-linked and show that every stem-linked tree forcing has the density property.
This is joint work with Philipp Schlicht, David Schrittesser and Thilo Weinert.
- 26 Jan 2017 » Arctic Set Theory Workshop - HOD in $M_n(x,g)$
On January 26th 2017 I gave a talk at the Arctic Set Theory Workshop 3 in Kilpisjärvi, Finland, about $\operatorname{HOD}$ in $M_n(x,g)$. Here are my (very sketchy!) slides.
The following pictures are taken by Andrés Villaveces. Thank you Andrés!




- 01 Dec 2016 » KGRC Research Seminar - $HOD^{M_n(x,g)}$ is a core model
On December 1st 2016 I gave a talk in the KGRC Research Seminar.
Abstract: Let $x$ be a real of sufficiently high Turing degree, let $\kappa_x$ be the least inaccessible cardinal in $L[x]$ and let $G$ be $Col(\omega, {<}\kappa_x)$-generic over $L[x]$. Then Woodin has shown that $\operatorname{HOD}^{L[x,G]}$ is a core model, together with a fragment of its own iteration strategy.
Our plan is to extend this result to mice which have finitely many Woodin cardinals. We will introduce a direct limit system of mice due to Grigor Sargsyan and sketch a scenario to show the following result. Let $n \geq 1$ and let $x$ again be a real of sufficiently high Turing degree. Let $\kappa_x$ be the least inaccessible strong cutpoint cardinal of $M_n(x)$ such that $\kappa_x$ is a limit of strong cutpoint cardinals in $M_n(x)$ and let $g$ be $Col(\omega, {<}\kappa_x)$-generic over $M_n(x)$. Then $\operatorname{HOD}^{M_n(x,g)}$ is again a core model, together with a fragment of its own iteration strategy.
This is joint work in progress with Grigor Sargsyan.

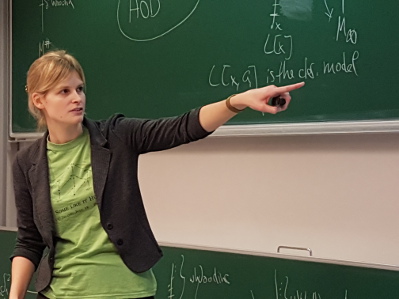

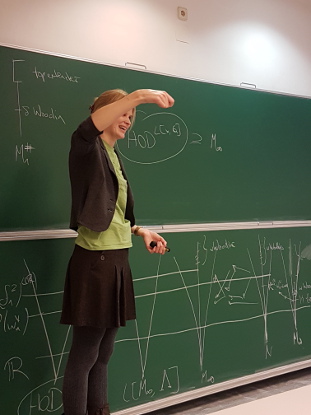



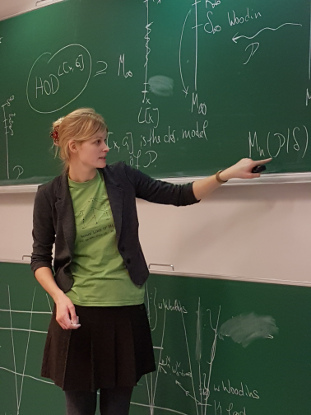
Many thanks to Richard again for the great pictures!
- 21 Oct 2016 » (with R. Schindler and W. H. Woodin) Mice with Finitely many Woodin Cardinals from Optimal Determinacy Hypotheses
Journal of Mathematical Logic. Volume 20, Issue Supp01, October 2020. 1950013.
DOI: 10.1142/S0219061319500132. PDF. arXiv. Bibtex. - 21 Oct 2016 » Graduation from the University of Münster
Last week I defended my PhD thesis and finally graduated from the University of Münster. Many thanks to everybody who was there to celebrate with me and especially to Anna, Dorothea, Fabiana and Svenja for the amazing graduation hat.
- 20 Oct 2016 » Pure and Hybrid Mice with Finitely Many Woodin Cardinals from Levels of Determinacy
- 19 Jul 2016 » 1st Irvine Conference on Descriptive Inner Model Theory and HOD Mice - Producing $M_n^{sharp}(x)$ from optimal determinacy hypotheses
On July 19th and 21st I gave talks at the 1st IRVINE CONFERENCE on DESCRIPTIVE INNER MODEL THEORY and HOD MICE.
Abstract: In this talk we will outline a proof of Woodin’s result that boldface $\boldsymbol\Sigma^1_{n+1}$ determinacy yields the existence and $\omega_1$-iterability of the premouse $M_n^\sharp(x)$ for all reals $x$. This involves first generalizing a result of Kechris and Solovay concerning OD determinacy in $L[x]$ for a cone of reals $x$ to the context of mice with finitely many Woodin cardinals. We will focus on using this result to prove the existence and $\omega_1$-iterability of $M_n^\sharp$ from a suitable hypothesis. Note that this argument is different for the even and odd levels of the projective hierarchy. This is joint work with Ralf Schindler and W. Hugh Woodin.
You can find notes taken by Martin Zeman here and here.

More pictures and notes for the other talks can be found on the conference webpage.
- 13 Jun 2016 » YSTW 2016 Copenhagen - A Journey Through the World of Mice and Games - Projective and Beyond
On June 13th, 2016 I gave a talk at the Young Set Theory Workshop in Copenhagen. For more information see the webpage of the YSTW 2016.
Abstract: This talk will be an introduction to inner model theory the at the level of the projective hierarchy and the $L(\mathbb{R})$-hierarchy. It will focus on results connecting inner model theory to the determinacy of certain games.
Mice are sufficiently iterable models of set theory. Martin and Steel showed in 1989 that the existence of finitely many Woodin cardinals with a measurable cardinal above them implies that projective determinacy holds. Neeman and Woodin proved a level-by-level connection between mice and projective determinacy. They showed that boldface $\boldsymbol\Pi^1_{n+1}$ determinacy is equivalent to the fact that the mouse $M_n^\sharp(x)$ exists and is $\omega_1$-iterable for all reals $x$.
Following this, we will consider pointclasses in the $L(\mathbb{R})$-hierarchy and show that determinacy for them implies the existence and $\omega_1$-iterability of certain hybrid mice with finitely many Woodin cardinals, which we call $M_k^{\Sigma, \sharp}$. These hybrid mice are like ordinary mice, but equipped with an iteration strategy for a mouse they are containing, which enables them to capture certain sets of reals. We will discuss what it means for a mouse to capture a set of reals and outline why hybrid mice fulfill this task.
- 09 Jun 2016 » KGRC Research Seminar - Hybrid Mice and Determinacy in the L(IR)-hierarchy
On June 9th 2016 I gave a talk in the KGRC Research Seminar in Vienna.
Abstract: This talk will be an introduction to inner model theory the at the level of the $L(\mathbb{R})$-hierarchy. It will focus on results connecting inner model theory to the determinacy of certain games.
Mice are sufficiently iterable models of set theory. Martin and Steel showed in 1989 that the existence of finitely many Woodin cardinals with a measurable cardinal above them implies that projective determinacy holds. Neeman and Woodin proved a level-by-level connection between mice and projective determinacy. They showed that boldface $\boldsymbol\Pi^1_{n+1}$ determinacy is equivalent to the fact that the mouse $M_n^\sharp(x)$ exists and is $\omega_1$-iterable for all reals $x$.
Following this, we will consider pointclasses in the $L(\mathbb{R})$-hierarchy and show that determinacy for them implies the existence and $\omega_1$-iterability of certain hybrid mice with finitely many Woodin cardinals, which we call $M_k^{\Sigma, \sharp}$. These hybrid mice are like ordinary mice, but equipped with an iteration strategy for a mouse they are containing, which enables them to capture certain sets of reals. We will discuss what it means for a mouse to capture a set of reals and outline why hybrid mice fulfill this task. If time allows we will sketch a proof that determinacy for sets of reals in the $L(\mathbb{R})$-hierarchy implies the existence of hybrid mice.



Many thanks to Richard for the pictures!
- 18 Jan 2016 » Hamburg Set Theory Workshop 2016 - Hybrid Mice with Finitely Many Woodin Cardinals from Determinacy
On January 18, 2016, I gave a talk at the Hamburg Set Theory Workshop 2016.
Hybrid Mice with Finitely Many Woodin Cardinals from Determinacy
Abstract: Mice are countable sufficiently iterable models of set theory. Hybrid mice are mice which are equipped with some iteration strategy for a mouse they are containing. This allows them to capture stronger sets of reals.
W. Hugh Woodin has shown in so far unpublished work that boldface $\Pi^1_{n+1}$-determinacy implies that $M_n^\sharp(x)$ exists and is $\omega_1$-iterable for all reals $x$. We will generalize parts of this to hybrid mice and levels of determinacy in the $L(\mathbb{R})$-hierarchy.
- 23 Sep 2015 » Minisymposium Set Theory, DMV-Jahrestagung, Hamburg - Mice with finitely many Woodin cardinals from optimal determinacy hypotheses
On September 23, 2015, I gave a talk in the Minisymposium Set Theory at the DMV-Jahrestagung in Hamburg.
Mice with finitely many Woodin cardinals from optimal determinacy hypotheses
Abstract: Mice are countable sufficiently iterable models of set theory. Itay Neeman has shown that the existence of such mice with finitely many Woodin cardinals implies that projective determinacy holds. In fact he proved that the existence and $\omega_1$-iterability of $M^{\sharp}_n(x)$ for all reals $x$ implies that boldface $\Pi^1_{n+1}$-determinacy holds.
We prove the converse of this result, that means boldface $\Pi^1_{n+1}$-determinacy implies that $M^{\sharp}_n(x)$ exists and is $\omega_1$-iterable for all reals $x$. This level-wise connection between mice and projective determinacy is an old so far unpublished result by W. Hugh Woodin. As a consequence we can obtain the determinacy transfer theorem for all levels $n$. These results connect the areas of inner model theory and descriptive set theory, so we will give an overview of the relevant topics in both fields and briefly sketch a proof of the result mentioned above. The first goal is to show how to derive a model of set theory with Woodin cardinals from a determinacy hypothesis. The second goal is to prove that there is such a model which is iterable. For this part the odd and even levels of the projective hierarchy are treated differently.
This is joint work with Ralf Schindler and W. Hugh Woodin
- 06 Jul 2015 » Oberseminar Bonn - Mice with finitely many Woodin cardinals from optimal determinacy hypotheses
On July 6st, 2015, I gave a talk in the Logik Oberseminar in Bonn.
Title: Mice with finitely many Woodin cardinals from optimal determinacy hypotheses
- 05 Mar 2015 » KGRC Research Seminar, Vienna - Mice with finitely many Woodin cardinals from optimal determinacy hypotheses
I gave a talk in the KGRC Research Seminar at University of Vienna on Mar 3rd, 2015.
Title: Mice with finitely many Woodin cardinals from optimal determinacy hypotheses
- 12 Dec 2014 » CUNY Set Theory Seminar - Producing $M_n^{sharp}$ from Boldface Level-wise Projective Determinacy
On Dec 12st, 2014, I gave a talk in the CUNY Set Theory Seminar.
Title: Producing $M_n^\sharp$ from Boldface Level-wise Projective Determinacy
- 21 Oct 2014 » Oberseminar Münster - Woodins HOD Conjecture
On October 21 and 28, 2014, I gave talks in the Mengenlehre Oberseminar in Münster.
Title: Woodins HOD Conjecture
- 16 Sep 2014 » Workshop in Set Theory, Bedlewo, Poland - Producing Iterable Inner Models with Finitely many Woodin Cardinals from Optimal Determinacy Hypotheses
On September 16th, 2014, I gave a talk in the Workshop in Set Theory in Bedlewo, Poland.
Title: Producing Iterable Inner Models with Finitely many Woodin Cardinals from Optimal Determinacy Hypotheses
- 05 Sep 2014 » Colloquium Logicum 2014, Neubiberg - Producing Iterable Inner Models with Finitely many Woodin Cardinals from Optimal Determinacy Hypotheses
On September 5th, 2014, I gave at talk at the Colloquium Logicum in Neubiberg.
Title: Producing Iterable Inner Models with Finitely many Woodin Cardinals from Optimal Determinacy Hypotheses
- 19 May 2014 » Oberseminar Münster - Producing ${M_n^{sharp}}$ from optimal determinacy hypotheses
On May 19, 2014, I gave a talk in the Mengenlehre Oberseminar in Münster.
Title: Producing $M_n^\sharp$ from optimal determinacy hypotheses
- 07 Mar 2014 » INFTY Final Conference, Bonn - Producing Inner Models with Woodin Cardinals from Projective Determinacy
On March 07, 2014, I gave a talk at the INFTY Final Conference in Bonn.
Title: Producing Inner Models with Woodin Cardinals from Projective Determinacy
- 12 Nov 2013 » Doktorandenforum der Studienstiftung des deutschen Volkes, Köln - Nicht-Beweisbarkeit und unendliche Spiele
On November 12th, 2013, I gave a talk (in German) in Köln at the Doktorandenforum of the Studienstiftung des deutschen Volkes (German National Academic Foundation).
Title: Nicht-Beweisbarkeit und unendliche Spiele
- 28 Oct 2013 » Oberseminar Münster - Producing $M_n^{sharp}$ from Projective Determinacy
On October 28 and November 04, 2013, I gave talks in the Mengenlehre Oberseminar in Münster.
Title: Producing $M_n^\sharp$ from Projective Determinacy
- 12 Jul 2013 » Graduate Summer School in Set Theory, Irvine - On a Generalization of a Lemma by Kechris and Solovay to an Inner Model Theoretic Context
On July 12th, 2013, I gave a talk at the Graduate Summer School in Set Theory in Irvine.
Title: On a Generalization of a Lemma by Kechris and Solovay to an Inner Model Theoretic Context
- 02 May 2013 » Tecklenburg - Games in Set Theory
On May 2nd, 2013, I gave a talk in Tecklenburg at a meeting for PhD students in mathematics at University of Münster.
Title: Games in Set Theory
- 22 May 2012 » Writeup of an account of Woodin’s HOD conjecture
Masterthesis (in German). PDF






